ریاضیدانانی که من می شناختم

این مقاله که ترجمه ایست از سخنرانی جورج پولیا و در مجله نشر ریاضی به چاپ رسیده است، پر است از حکایتهای جالب درباره ریاضیدانان. خواندن آن را به همه توصیه میکنم.

اثبات آبکی قضیه فیثاغورس

داستان مربعی که سه تا بود

این مقاله جالب نوشته خانم لیلا خسروشاهی در مجله برهان چاپ شده است. 

یک بازی جالب که توسط یکی از دانش آموزان معرفی شده

این بازی رو افرا معرفی کرده است. شما باید سعی کنید مساحت بیشتری را رنگ کنید تا برنده بشید.

http://www.gamedesign.jp/flash/fourcolor/fourcolor.html

 

آندره زیمردی، ارباب الگوهای ریاضی برنده جایزه یک میلیون دلاری آبل

تصور کنید که من به شما یک ردیف کارت نشان دهم که با شماره‌های 1 تا n برچسب گذاری شده‌اند و در آن n عدد خیلی بزرگی است. از شما می‌خواهم که تعداد مشخصی از کارت‌ها را بردارید؛ این که کدام کارت‌ها را بردارید بسته به شما است، و یک سری شکاف تصادفی خیلی زشت و اجتناب‌ناپذیر در توالی کارت‌هایی که به دقت چیده بودم پدید می‌آورد. به نظر می‌رسد که نظم و ترتیب به طور کامل از بین رفته باشد، ولی در حقیقت هیچ اهمیتی ندارد که شما کدام کارت‌ها را بردارید، من همیشه می‌توانم الگوی کاملا منظمی را در اعدادی که باقی مانده‌اند، پیدا کنم.

به عنوان یک شعبده بازی شاید این کار با هیجان نصف کردن یک انسان از وسط برابری نکند(!)، اما اثبات ریاضی این نکته که همواره می‌توان در چنین وضعیتی یک الگوی ریاضی یافت، یکی از مسائلی است که باعث شد ریاضیدانی به نام آندره زیمردی، برنده جایزه معتبر آبل ریاضیات در سال 2012 شود.
به گزارش نیوساینتیست، فرهنگستان علوم و ادبیات نروژ در اسلو، جایزه یک میلیون دلاری آبل را برای «نقش بنیادین در ریاضیات گسسته علوم نظری کامپیوتر» به زیمردی اهدا کرد. تخصص او ترکیبیات(تعیین تعداد راه‌های انجام یک کار) است، حوزه‌ای که با راه‌های مختلف شمارش و بازآرایی موضوعات گسسته سر و کار دارد، حال چه عدد باشد و چه کارت بازی.
حقه‌ای که در بالا توصیف شد، نتیجه مستقیم چیزی است که به نام نظریه زیمردی شناخته می‌شود، بخشی از ریاضیات که به سوالی پاسخ می‌دهد که اولین بار توسط دو ریاضیدان به نام‌های پل اردوس و پال توران در سال 1936 / 1315 مطرح شد و به مدت تقریبا 40 سال بی پاسخ مانده بود.
ذهن بی قاعده این نظریه نشان می‌دهد که چگونه می‌توان در مجموعه‌های بزرگ اعداد متوالی الگوها را یافت، حال هر تعداد از اعداد آنها که حذف شده باشند. الگوهای مورد سوال، توالی‌های محاسباتی هستند (زنجیره‌هایی از اعداد با اختلاف یکسان، مانند 3، 7، 11، 15، 19).
طرح چنین مسائلی معمولا برای ریاضیدان‌ها خیلی ساده ولی حل آنها بسیار سخت است. در کتاب «یک ذهن بی‌قاعده»، که در سال 2010 / 1389و به مناسبت هفتادمین سالگرد تولد زیمردی منتشر شد، گفته شده که «مغز او کاملا متفاوت با دیگر ریاضیدان‌ها سیم‌بندی شده است».
تیموتی گاورز، ریاضی‌دانی از دانشگاه کمبریج، که بعد از اعلام برنده شدن زیمردی در اسلو سخنرانی کرده، می‌گوید: «او بیشتر از هر کس دیگری، به سراغ ایده‌های عجیب و غیر معمول می‌رود».
زیمردی عملا دیر وارد دنیای ریاضیات شد، او در ابتدا یک سال در دانشکده پزشکی درس خواند و بعد از آن نیز تا پیش از آنکه تصمیم به تحصیل در رشته ریاضیات بگیرد، مدتی در یک کارخانه کار کرد. استعداد او توسط اردوس کشف شد که به کار با صدها ریاضیدان در طول عمر خود شهره بود.
برنده فروتن هنگامی که زیمردی نظریه خود را در سال 1975/ 1354 ثابت کرد، یک ابزار ریاضی به نام قیاس ترتیب زیمردی را نیز به ریاضیدان‌ها عرضه کرد که درک عمیق‌تری از گراف‌های بزرگ‌تر می‌دهد. اگر از درس‌های ریاضیا جدید یا ریاضیات گسسته دورا دبیرستان به یادتان ماده باشد، گراف به موضوع‌های ریاضی گفته می‌شود که عموما از آنها برای مدل سازی ساختارهای شبکه‌ای مانند اینترنت از آنها استفاده می‌شود.
قیاس همچنین به دانشمندان علوم کامپیوتر کمک کرده تا به درک بهتری از شیوه‌ای در هوش مصنوعی دست یابند که «آموزش احتمالا تقریبا صحیح» نامیده می‌شود. زیمردی همچنین بر روی یک مساله محاسباتی مهم دیگر مربوط به مرتب کردن فهرست‌ها کار کرده، که یک حد نظری را برای مرتب‌سازی با استفاده از پردازنده‌های موازی که در کامپیوترهای امروزی پیدا می‌شوند، اثبات می‌کند.

یک معمای توپولوژیکی

به این آدرس بروید و این معمای جالب را حل کنید. اگر در خانه هستید دیگران را هم به چالش بکشید.

یک معمای توپولوژیکی

مطابق شکل دستهاتونو با دو تا نخ یا طناب، به هم گیر بدهید.

حالا سعی کنید گیر طناب را برطرف کنید و از هم جدا بشید. راه‌حل در آینده‌ای نزدیک رونمایی خواهد شد!

یک فیلم کوتاه درباره اعداد به ویژه اعداد فیبوناچی

 این فیلم کوتاه را از دست ندهید.

مروری بر اتحادها

در این مقاله کوتاه که برای سال اولی‌ها مناسب است مروری کوتاه بر اتحادها خواهیم داشت. این مقاله از مجله برهان انتخاب شده است. سال اولی‌ها حتماً این مقاله را بخوانند.  

اصل لانه کبوتر یا اصل حجره‌ها

در این مقاله که در مجله کوشیار به چاپ رسیده است؛ با اصل ساده اما پرکاربرد لانه کبوتر آشنا می‌شوید.  

300 مساله در مثلثات

در این جزوه 300 مساله در مثلثات گردآوری شده است. با حل این مساله ها توانایی خود را در مثلثات افزایش دهید.

   

استاد پرویز شهریاری درگذشت

پرويز شهرياري، استاد رياضيات و سردبير مجله‌هاي «وهومن» و «چيستا» پس از ٨٦ سال زندگي پربار علمي و فرهنگي در بیمارستان جم در گذشت. وي كه پيش از اين نيز، چند بار دچار حمله‌ قلبي و مغزي شده ‌بود، بامداد جمعه (22 اردیبهشت) بر اثر سكته‌ قلبي چشم از جهان فروبست. 

شهرياري در سال ١٣٤٥، نشان درجه يك علمي و در سال ١٣٨٤ به عنوان چهره‌ ماندگار جمهوری اسلامی ايران در رشته ریاضیات شناخته شد، وی همواره می گفت: رياضي پايه تمامي علوم است و در واقع اگر کسي رياضي بداند، مي‌تواند در همه‌ دانش‌ها سررشته‌ داشته باشد و كار بكند. 

پرويز شهرياري، رياضيدان و چهره‌ ماندگار ریاضی ایران، در سال 1305 خورشيدي در كرمان زاده شد. پدر شهرياري دهقان ‌زاده‌اي بود که روي زمين‌هاي اربابي کارگري مي‌کرد. بعد از مرگ پدر، مسووليت خانواده به عهده مادر او (گلستان شهرياري) بود. اين خانواده از لايه‌هاي درآمدي پايين جامعه بودند و دوران کودکي شهرياري دوران سختي از نظر معيشتي بود.

وي تا سال سوم دبيرستان را در دبيرستان ايرانشهر در شهر کرمان گذراند و وارد دانشسراي مقدماتي کرمان شد. در خرداد ۱۳۲۳ فارغ‌التحصيل شد و براي ادامه تحصيل به تهران آمد. در تهران در سال ۱۳۳۲ در رشته رياضي از دانشکده علوم دانشگاه تهران و دانش‌سراي عالي (دانشگاه تربيت معلم تهران کنوني) فارغ‌التحصيل شد. يک سال در شيراز معلم بود و در ۱۳۳۳ به تهران آمد. آن روزها در دبيرستان انديشه و دبيرستان‌هاي مربوط به گروه فرهنگي خوارزمي درس مي‌داد و در دانشکده فني دانشگاه تهران، در کلاس‌هاي روزانه و شبانه دانشگاه تربيت معلم و در اراک در مدرسه عالي علوم اراک هم مشغول تدريس بود.

شهرياري، آموزگار و نويسنده خستگي‌ناپذيري بود كه تاليفات و ترجمه‌هايش در حوزه دانش رياضي، ادبيات و فلسفه به بيش از صدها عنوان مي‌رسند و بي‌گمان هر كس كه در ايران دوستدار رياضيات باشد از آثار وي بي‌بهره نبوده است.

از اين استاد بزرگ بيش از صد عنوان كتاب درسي رياضيات، از جمله دوره‌ كتاب‌هاي درسي رياضي سه سال اول دبيرستان نظام قديم، دوره‌ كامل رياضيات دبيرستاني و كتاب‌هاي مسايل مربوط به آن و جبر سال سوم رشته‌ رياضي فيزيك و سه جلد كتاب آناليز رياضي، بيش از 97 كتاب كمك درسي به صورت ترجمه و تاليف، حدود 20 كتاب در زمينه‌هاي مختلف تاريخ، فلسفه، كاربرد و آموزش رياضيات و 9 جلد كتاب سرگرمي در رياضيات به دانش‌آموزان و دانش‌پژوهان رياضي كشور ارايه شده اند.

استاد شهرياري علاوه بر اين آثار، كتاب های ديگری در زمينه‌هاي مختلف تاليف يا ترجمه كرده‌ كه در اين باره مي‌توان به كتاب‌هاي «دانشمندان و هنرمندان»، «خانه‌ اهريمن»، «دانش و شبه دانش»، «دو درس كوتاه درباره‌ ديرين‌شناسي»، «قطاري كه در بعد چهارم گم شد» و «نظريه‌ نسبيت در مساله‌ها و تمرين‌ها» اشاره كرد.

«تاريخ حساب»، «رياضيات در شرق»، «سرگذشت آناليز رياضي»، «رياضيات کار بسته»، «لباچوسکي و هندسه نااقليدسي»، «پويايي رياضيات»، «من رياضي‌دانم»، «آفرينندگان رياضيات عالي»، «خلاقيت رياضي»، «عالي جناب چکمه (گوشه‌اي از تاريخ رياضيات)»، «سرگذشت رياضيات»، «لگاريتم (تاريخ استدلالي لگاريتم)»، «هندسه در گذشته و حال»، «غياث‌الدين جمشيد کاشاني رياضي‌دان ايراني»، «جوهر، روش و کارآيي رياضيات»، «فلسفه، اخلاق و رياضيات»، «خلاقيت در رياضيات و مهندسي»، «رياضيات و هنر»، «آموزش رياضي»، «گاهنامه رياضي، شامل شرح حال و نظر رياضي‌دانان»، «شما هم مي‌توانيد در درس رياضي خود موفق باشيد»، «نگاهي به تاريخ رياضيات در ايران» و... عناوين كتاب‌هاي شهرياري محسوب مي‌شوند.

پيكر اين استاد زرتشتي، 22 اریبهشت ساعت ١٦ در آرامگاه زرتشتيان تهران در قصر فيروزه به خاك سپرده شد. روحش شاد و یادش گرامی باد.

برای مطالعه زندگینامه پربار استاد رجوع شود به

http://fa.wikipedia.org/wiki/پرویز_شهریاری

سوالهای آزمون گزینش المپیاد ریاضی و کامپیوتر

این آزمون چهارشنبه سیزدهم اردیبهشت برگزار شد. سوالهای آزمون را میتوانید از اینجا دانلود کنید. راستی متوجه شدید که راه‌حل مساله سه، پایین صفحه درج شده بود؟!

گریگوری پرلمان کیست ؟

گريگوري ياكولويچ پرلمان ( گريشا پرلمان ) متولد ۱۳ژوئن ۱٩۶۶ در لنينگراد (سن پترزبورگ كنوني) رياضيداني روسي است كه بواسطه ي تلفيق هندسه ريماني و توپولوژي هندسي نقطه عطفي را در تاريخ رياضيات موجب گرديده است . به ويژه اينكه اثبات وي از حدس هندسي تورستن منجر به حل حدس مشهور پوانكاره شده است كه به عنوان يكي از مشكل ترين مسائل تاريخ رياضيات شناخته شده بود . اين حدس نخستين بار توسط رياضيدان فرانسوي ژولز هانري پوانكاره در ۱٩٠۴مطرح گرديد و هدف آن فهم شكل عالم بكمك اشكال ، فضاها و سطوح بهم پيوسته است .

در آگوست ٢٠٠۶ پرلمان براي تركيب هندسه با ايده‌هاي انقلابي خود در مورد ساختار تحليلي و هندسي شارش ريچي برنده ي مدال فيلدز شد اما وي از دريافت جايزه و حتي شركت در كنگره مربوطه امتناع نمود . در ٢٢ دسامبر همان سال مجله ساينس اثبات پرلمان از حدس پوانكاره را بزرگترين كشف علمي سال لقب داد كه در عالم رياضيات بي‌سابقه بوده است .

گريگوري پرلمان در خانواده اي يهودي چشم به جهان گشود . آموزشهاي مقدماتي رياضي را در دبيرستان لنينگراد كه دوره هاي ويژه ي رياضي و فيزيك داشت سپري نمود و در سال ۱٩۸٢ به عنوان يكي از اعضاي تيم ملي المپياد رياضي شوروي برگزيده شد و به خاطر كسب نمره ي كامل مدال طلا در يافت كرد . وي در اواخر دهه ي ۱٩۸٠ از دانشكده ي رياضيات و مكانيك دانشگاه لنينگراد كه يكي از دانشگاههاي ممتاز شوروي سابق بود به درجه ي Ph.d نائل شد . عنوان تز دكتراي وي عبارت بود از : سطوح زيني در فضاهاي اقليدسي.

وي پس از فارغ التحصيل شدن كارش را در انستيتو رياضي استكلوف در آكادمي علوم تحت نظر مشاورينش الكساندر دانيلويچ الكساندروف و يوري ديميتريويچ بوراگو آغاز نمود . وي در سال ۱٩٩٢ براي گذراندن يك نيمسال تحصيلي به دانشگاههاي نيويورك و استوني بروك دعوت شد . همچنين از سوي چندين دانشگاه برجسته ي ايالات متحده نظير پرينستون و استانفورد به وي پيشنهاد كار شد كه او هيچكدام را نپذيرفت و در ۱٩٩۵ پس از گذراندن بورسيه ي تحصيلي ميلر از دانشگاه بركلي كاليفرنيا (در ۱٩٩۳) به انستيتو استكلوف بازگشت . 

پرلمان از راه تدريس درآمد كمي دريافت مي كند و با اينحال براي پذيرفتن جايزه ي يك ميليون دلاري كه از سوي انستيتو رياضي كلي پيشنهاد شده است كاملا ً اظهار بي ميلي دارد . در مصاحبه با پرلمان وي تاكيد داشته كه لايق اينهمه توجه نيست و نسبت به جوايزي كه به وي پيشنهاد گرديده بي علاقه است . او به همراه مادرش در آپارتماني كوچك در سن پترزبورگ و با حق بازنشستگي مادرش كه ماهيانه در حدود ۵۷ دلار است زندگي مي كند .

 

اعداد تاکسی

زمانی كه ریاضیدان انگلیسی هاردی برای عیادت ریاضیدان شهیر هند رامانوجان به بیمارستان رفته بود به این موضوع اشاره كرد كه شماره تاكسی كه به وسیله آن به بیمارستان آمده، عدد بی ربط و بی خاصیت 1729 بوده است . رامانوجان بلافاصله ضمن رد ادعای هاردی به او یادآور شد كه اتفاقا 1729 بسیار جالب توجه است . خود ۱۷۲۹ عدد اول است.بقیه در ادامه مطلبدو عدد ۱۷ و ۲۹ هر كدام عدد اول هستند. جمع چهار رقم تشكیل دهنده آن میشود ۱۹ كه اول است.جمع دو عدد اولیه و دو عدد آخری میشود ۸۱۱ كه باز هم عدد اول است دو عدد ابتدایی(سمت چپ) اگر جمع شوند؛عدد ۸۲۹ میشود كه باز هم عدد اول است.دو عدد اولیه اگر از هم دیگر كسر شوند؛عدد ۶۷ ساخته میشود كه باز هم عدد اول است. سه عدد سازنده آن عدد اول است(۱و۷و ۲).عدد اول؛عددی است كه فقط بر یك و خودش تقسیم میشودبنحوی كه نتیجه تقسیم عددی كسری نباشد(خارج تقسیم نداشته باشد)جمع عددی اعداد تشكیل دهنده ۱۷۲۹ یا:۱+۷+۲+۹=۱۹ است؛ عكس ۱۹ عدد ۹۱ است؛ اگر۱۹*۹۱بشود نتیجه برابر ۱۷۲۹ میشود.این هم یكی دیگر از اختصاصات ۱۷۲۹ است كه در هر عددی دیده نمیشود.عدد 1729 اولین عددی است كه می توان آنرا به دو طریق به صورت حاصلجمع مكعبهای دو عدد مثبت نوشت :به توان 3 به علاوه 1 به توان 3 و 10 به توان 3 به علاوه 9 به توان 3 هردو برابر 1729 می باشند .(اولین مطلب موجود در رابطه با این خاصیت 1729 به كارهای بسی ریاضیدان فرانسوی قرن هفدهم باز می گردد.)

حال اگر كمی مانند ریاضیدانها عمل كنید باید به دنبال كوچكترین عددی بگردید كه به سه طریق مختلف حاصلجمع مكعبهای دو عدد مثبت است این عدد 87539319 می باشد كه در سال 1957 توسط لیچ كشف شد: 414 به توان 3 + 255 به توان 3 و 423 به توان 3+ 228 به توان 3 و 436 به توان 3 + 167 به توان 3 هر سه جوابشان برابر 87539319 است .امروزه ریاضیدانان عددی را كه به n طریق مختلف به صورت حاصلجمع مكعبهای دو عدد مثبت باشد ،n ــامین عدد تاكسی می نامند و آنرا با Taxicab نمایش می دهند.جالبتر از همه اینكه ،هاردی و رایت ثابت كردند برای هر عدد طبیعی n ناكوچكتر از 1 ،n ــامین عدد تاكسی وجود دارد ! هرچند، چهارمین تا هشتمین اعداد تاكسی نیز كشف شده اند ولی تلاشها برای یافتن نهمین عدد تاكسی تاكنون نا كام مانده است . متاسفانه اطلاعات زیادی درباره اعداد تاكسی موجود نیست . در ضمن میتوان مسئله را از راههای دیگر نیز گسترش داد . مثلا همانگونه كه هاردی در ادامه داستان فوق از رامانو جان پرسید و او قادر به پاسخگویی نبود ، این پرسش را مطرح كنید: كوچكترین عددی كه به دوطریق حاصلجمع توانهای چهارم دو عدد مثبت می باشد ،كدام است؟ این عدد توسط اویلر یافت شده است : 635318657 حاصلجمع توان چهارم 59 و 158 همچنین توانهای چهارم 133 و 134 می باشد.  

دریاره سودوکو

در این مقاله  که در آخرین شماره مجله ریاضیات به چاپ رسیده با معمای سودوکو, تاریخچه آن و ریاضیات مرتبط با آن, روشهای حل آن و سایت های مرتبط با این موضوع آشنا میشوید. خواندن این مقاله را به همه دانش‌آموزان توصیه میکنم.  

یک مساله جالب برای دانش‌آموزان اول

در یک جنگ ۱۰۰ سرباز شرکت کردند و جراحاتی برداشتند. آمار جراحات به شرح زیراست:

۷۰ نفر دست راستشان را از دست دادند

۷۵ نفر دست چپشان را از دست دادند

۸۰ نفر پای راست و

 ۸۵ نفر پای چپ‌شان را از دست دادند.

 حداقل تعداد افرادی که هر ۴ عضوشان را از دست داده‌اند چندتاست؟

اتحادهای مثلثاتی

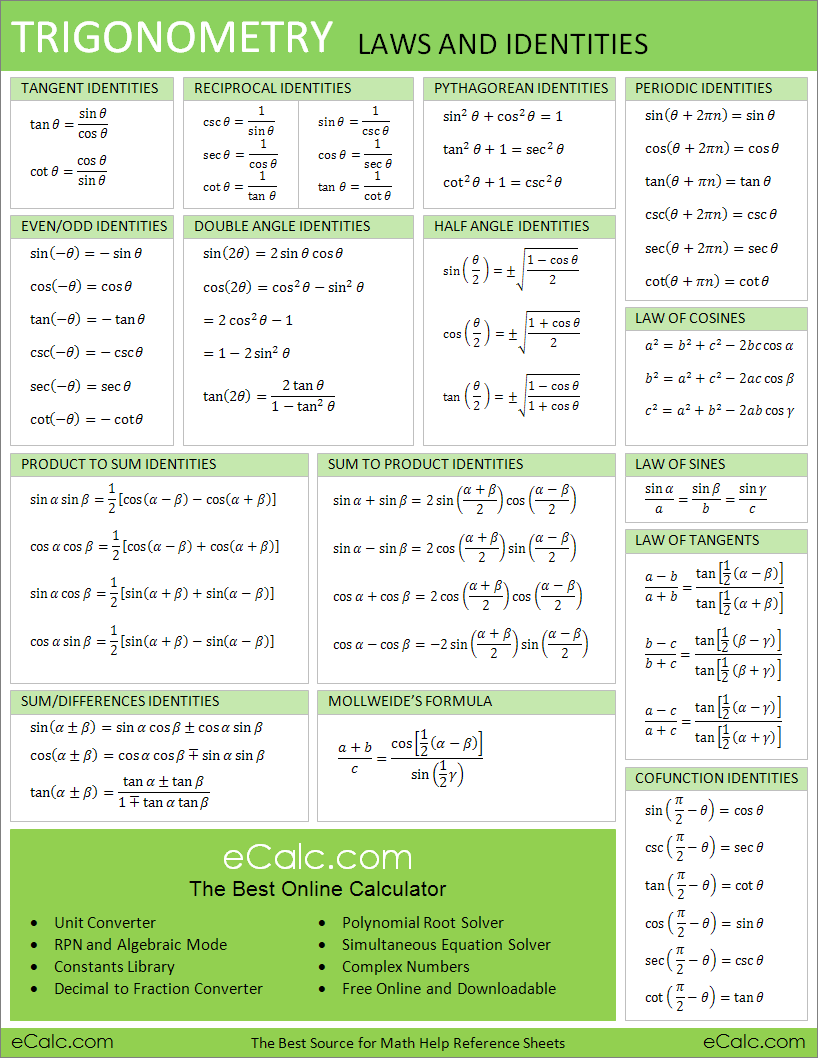
در این مقاله که در شماره نوزدهم مجله برهان چاپ شده است شما با اتحادهای مثلثاتی و کاربرد آنها در حل مسائل آشنا می‌شوید. در مجموع 31 مثال و مساله و تست در این مقاله ذکر شده است. برای دانلود پوستر زیر روی تصویر راست کلیک کنید و تصویر را روی کامپیوتر خود ذخیره کنید.  

افتخارآفرینی تیم ربوکاپ آزاد دبیرستان فرزانگان 2 در هفتمین دوره مسابقات بین المللی ربوکاپ آزاد ایران

تیم ربوکاپ آزاد دبیرستان فرزانگان دو متشکل از خانمها (1) زهرا پژم, (2) رویا گلریز, (3) پرستو سمندی, (4) شقایق افراسیابی, (5) زهرا منوچهری, (6) مونا نیکخو, (7) مریم بختیاری, (8) پریشاد بهنام قادر, (9) پریسا حکمت نژاد, (10) سها حاجی فتحعلی, (11) غزاله شاهسون, (12) سارا نوری‌زاده, (13) مائده صلح‌جو, (14) آمنه محسن خیام, (15) عطیه زارع, (16) گیتا سرفراز, (17) سبا کابلی‌نژاد و (18) گلبرگ یگانه موفق به کسب رتبه دوم در هفتمین مسابقات ربوکاپ آزاد ایران در بخش روبات‌های نمایشی (تیم های دانش‌آموزی پیشرفته) شدند.

این موفقیت را به همه این عزیزان, همکلاسی های آنان, خانواده‌های آنان و اولیاء مدرسه تبریک می‌گوییم.

65 مساله از فصل سوم کتاب ریاضی تکمیلی سال اول

از اینجا می‌توانید 65 مساله از فصل سوم کتب ریاضی تکمیلی چاپ انتشارات خیـــــــــــــــــــــــــــــــــلی سبز را بارگذاری کنید و حل کنید.

معرفی سایت های ریاضی (5) : Brightstorm سایتی با فیلمهای آموزشی

در این سایت آموزشی شما می توانید از 2000 فیلم آموزشی که در زمینه ریاضیات و به صورت موضوعی طبقه بندی شده است استفاده کنید. به همه توصیه می کنم که بعد از یادگیری هر بخش از کتاب به این سایت سری بزنید و فیلمهای مرتبط را ببینید. یک فایده دیگر این فیلمها آموزش زبان انگلیسی است.  

بخش‌پذیری چندجمله‌ای‌ها

در این مقاله که در مجله برهان به چاپ رسیده است, شما با مفهوم بخشپذیری چندجمله‌ایها آشنا می‌شوید. پس از مطالعه مقاله؛ مساله زیر را حل کنید که 5 امتیاز دارد و مهلت آن تا بیستم فروردین است.

چندجمله‌ای درجه سوم f را بیابید به طوری که f(3)=6 و برای هر x داشته باشیم:

(x-2).f(x+1)=(x+1).f(x)

ریشه‌های خارجی معادله

در حل معادلات گوناگون, از جمله معادلات اصم و معادلات شامل لگاریتم دانش‌آموزان پیش از شروع به حل معادله, به یافتن حدود قابل فبول برای متغیر می‌پردازند. در پایان و پس از حل معادله, جواب‌های به‌دست‌آمده را با دامنه‌ای که در ابتدا یافته‌اند, مقایسه می‌کنند. در این مقاله که در مجله برهان به چاپ رسیده است, نویسنده به این موضوع پرداخته است.

آموزش ریاضی لذت بخش میشه اگه . . .

بدون توضیح!

معرفی سایت های مفید (3)

سایت "گره را ببر" (Cut the knot) یکی از بهترین سایت هایی است که درباره ریاضیات راه‌اندازی شده است. این سایت تاکنون چهل جایزه جهانی را از آن خود کرده است. برای استفاده از مطالب سایت می‌توانید از فهرست موضوعی که در ستون سمت چپ (صفحه اول سایت) موجود است اشتفاده کنید.  

حرکت با چرخهای چهارگوش

از اینجا مقاله را دانلود کنید و بخوانید (و حرکت با چرخهای چهارگوش را ببینید!)

اثبات اتحاد مزدوج

از اینجا دانلود کنید و ببینید.

نمایش اعداد صحیح در مبناهای مختلف

یکی از کاربردهای قضیه تقسیم, در نمایش اعداد صحیح در مبناهای مختلف است. این مقاله از مجله برهان انتخاب شده است و برای همه به خصوص سال چهارمی ها مفید است. اما پس از مطالعه مقاله, مساله زیر را حل کنید که 10 امتیاز دارد و تا بیستم فروردین هم فرصت دارید.

پنج کیسه داریم که داخل هرکدام سکه‌هایی هم‌وزن وجود دارد. وزن هر سکه ازهر کیسه مشخص نیست اما میدانیم عددی صحیح و کوچکتر از 20 است. سکه ها از لحاظ ظاهری تفاوتی با هم ندارند و همه شبیه هم هستند. همچنین ترازویی یک‌کفه‌ای داریم که تنها می‌توانیم یک بار از آن استفاده کنیم. با  این مفروضات مشخص کنید که وزن هر سکه از هر کیسه چقدر است. داخل هر کیسه, به هر اندازه که شما لازم داشته باشید سکه موجود است.

هل من مزید (2) : ده مساله از رادیکال و معادله خط

این تمرینات برای سال اولی هاست.  حل این تمرینات 30 امتیاز دارد و مهلت تحویل تا بیستم فروردین ماه است.